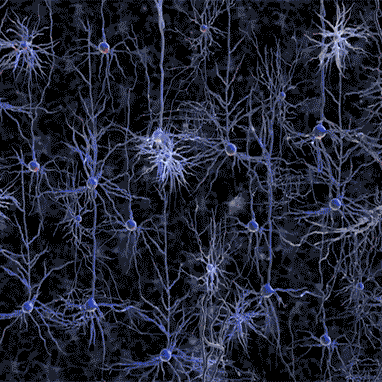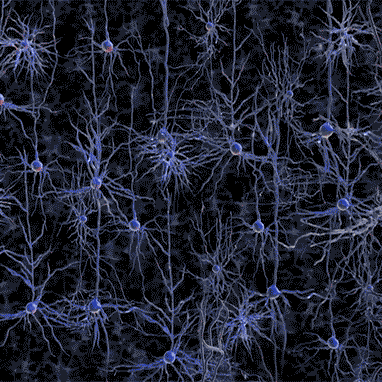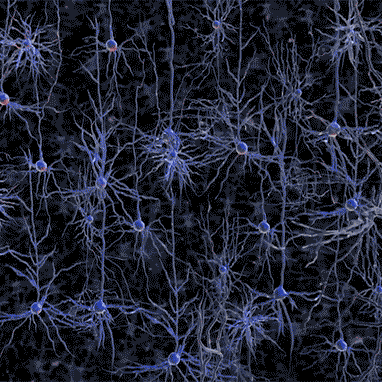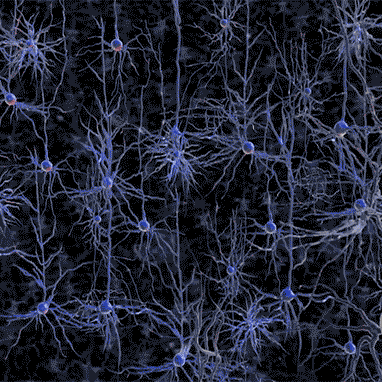
Теория игр как универсальный способ исследования мировых процессов

Вас и вашего сообщника задержали во время крупного ограбления и теперь допрашивают в разных комнатах. Если вы оба будете молчать, то каждый из вас получит, как минимум, год тюрьмы. Если вы оба признаетесь о содеянном, то получите по пять лет. Но если сознается лишь один из вас, то он выйдет на свободу, а второй получит 10 лет. Вы не знаете, что сделает ваш сообщник. Как поступить?

Эта задачка, известная как дилемма заключенного, является наиболее известным примером игры, в техническом смысле олицетворяющей теорию игр.

Теория игр представляет собой математический способ описания стратегического мышления, а дилемма заключенного иллюстрирует три основных требования ситуации: игра должна иметь несколько действующих лиц (в данном случае два сообщника), каждый должен принять решение (выдать или нет), каждое решение имеет свои последствия (тюремное заключение), которые изменяются в зависимости от решений других персонажей.

Только за последние восемь лет Нобелевская премия трижды уходила к теоретикам игр, которые смогли пролить свет на логику ядерного сдерживания, обстоятельства, при которых свободные рынки могут максимизировать общественное благосостояние, решение «проблемы соответствия» органов и пациентов.

Также в последнее время теория игр активно используется в области техники и информатики. Исследователи используют ее для анализа сложных проблем, таких как оптимизация транспортных потоков или предотвращения отключений.

Азу Оздаглар, профессор электротехники и компьютерных наук, говорит, что к этому привел рост областей охвата интернета. Исторически сложилось так, что инженерам сетей связи приходится решать широкий спектр технических вопросов, таких как ограничения по мощности и проблемы централизации и децентрализации.

Но с появлением интернета им пришлось столкнуться еще и с человеческим фактором. Если, предположим, абонент «Домолинк» в Москве и абонент «Билайн» в Перми обмениваются данными, то эта информация путешествует по сети через несколько провайдеров: «Домолинк», «Билайн» и ряд других.

Азу Оздагларпрофессор электротехники и компьютерных наук, MIT

Весь этот процесс зависит и от сотрудничества и от конкуренции различных сторон. Как создать протоколы, которые будут стимулировать людей к сотрудничеству?

Другими словами, почему интернет работает, ведь он состоит из отдельных сетей? Теория игр может помочь ответить на этот вопрос.

Когда инженеры начали использовать теорию игр для решения вопросов своей области, стало понятно, что приемы их работы вполне применимы к нерешенным вопросам теории игр. И действительно, несколько исследователей из Департамента электротехники и компьютерной науки (EECS), активно использующих теорию игр, потратили много времени на решение проблем, относящихся, казалось бы, к социальным наукам.

Попробовав раз

Профессор EECS Константинос Даскалайкис является ярким тому примером. В 2008 году он выиграл премию Ассоциации вычислительной техники, показав, что теоретическая информатика может пролить свет на одно из центральных понятий в теории игр: равновесие.

Идея равновесия принесла Нэшу Нобелевскую премию, и именно его равновесие является объектом наиболее пристального изучения. Оно описывает идеальную стратегию, которую у игроков нет мотива менять.

Самый простой пример равновесия Нэша включает в себя так называемую игру-пенальти. В футболе во время пенальти вратарю приходится угадывать, куда полетит мяч после удара. В теоретико-игровой версии, если оба игрока выберут одну и ту же половину ворот, то победит вратарь, а если разные, то победит бьющий.

Состояние равновесия в этой игре для обоих игроков состоит в случайном выборе направления удара, этот выбор они осуществляют с одинаковой частотой. Вероятность выигрыша у каждого игрока составляет 50%. При этом изменив свою стратегию, игроки едва ли увеличат свои шансы на успех. Например, если вратарь вдруг начал выбирать то же направление, что и бьющий, последний это заметит и изменит свой выбор. Таким образом, смысла менять стратегию нет.

Игра-пенальти – это одна из самых простых игр. Поиск равновесия даже для чуть более сложной игры может быть чрезвычайно трудным. В своей диссертации Даскалайкис доказал, что для некоторых ситуаций, которые могут быть описаны теорией игр, равновесие по Нэшу так трудно вычислить, что даже все компьютеры в мире никогда не смогут этого сделать. В таких случаях, как утверждает Даскалайкис, даже метод проб и ошибок не поможет. Это означает, что теоретикам игр нужны аналитические приемы, отличные от равновесия Нэша, если они хотят иметь хотя бы возможность описать реальный мир.

К счастью, информатика уже разработала ряд методов определения сложности вычислений, таких как те, которые находят равновесие Нэша, а также методы приблизительного решения сложных задач. Так, Даскалайкис и его ученики смогли найти решение проблемы, которая мучила экономистов последние 30 лет.

В 1981 году Роджер Майерсон из Университета Чикаго объяснил, как структурировать аукцион для одного лота, когда все участники торгов придерживаются своих интересах, чтобы продавец смог спрогнозировать наибольшую прибыль. Эта работа помогла ученому получить Нобелевскую премию в 2007 году. Он также затронул связанный с этим вопрос о том, как наилучшим способом построить аукцион для нескольких лотов (на языке экономистов, любой рынок с одним продавцом и несколькими покупателей - это аукцион. Например, аукцион Кристи или распродажа в розничном магазине).

Константинос ДаскалайкисПрофессор EECS

Это слишком сложный вопрос, чтобы дать конкретное описание аукциона с оптимальной для вас прибылью

Чтобы увеличить доход с нескольких лотов, продавцу, вероятно, следует продавать каждый лот по самой высокой цене, которую только могут предложить. Однако на прибыль может повлиять система скидок, например, за покупку нескольких лотов, за которыми тянутся покупатели.

Информатика предлагает свежий взгляд на проблему, которую Даскалайкис называет «приближенной перспективой».

Константинос ДаскалайкисПрофессор EECS

Может быть, вы не в состоянии представить оптимальный аукцион, но аукцион, который гарантирует 99% максимального дохода, тоже вполне хорош

Даскалайкис и его ученики продемонстрировали, что для любого рынка нескольких товаров идеальный аукцион (тот, который может принести максимально возможный доход) может быть приближен с помощью сочетания результатов более простых аукционов.

Несколько иной подход к проблемам аукциона демонстрирует профессор инженерии Сильвио Микали. Он и профессор EECS Шафи Гольдвассер - лауреаты последней премии Тьюринга, высшей награды в области компьютерных наук. В значительной степени награда вручается за так называемую интерактивную проверку, в ходе которой спрашивающий с ограниченными вычислительными ресурсами пытается выявить результат из вычислений от ненадежного собеседника с неограниченными вычислительными ресурсами. Одним из примеров является доказательство с нулевым разглашением, в котором один из участников устанавливает факт владения информацией, как криптографический ключ, не зная что это. Доказательства с нулевым разглашением используются для проверки безопасности между финансовыми учреждениями, а также стартапами для коммерциализации.

Микали работает над несколькими исследовательскими проектами в области теории игр, один из которых очень близок по духу доказательству с нулевым разглашением. Во время большинства публичных торгов продавец обязан раскрывать ставки всех участников.

Сильвио Микалипрофессор инженерии

Для компании, которая участвует в таких аукционах и проигрывает, это действительно худший из всех возможных вариантов. Ваши конкуренты теперь знают, насколько вам был ценен этот лот, а значит, они смогут сделать вывод о размере вашей клиентуры и доступных технологиях

Группа Микали работает над аукционами, в которых участники могут публично раскрывать часть информации о своих предложениях, чтобы определить победителя, не называя непосредственно ставку.

Сильвио Микалипрофессор инженерии

Я считаю, что это, в конечном итоге, станет основной в теории игр. Мы не можем предвидеть линию человеческого поведения без учета частной жизни

Кто под контролем?

Для многих ситуаций, которые могут быть представлены в виде игры, равновесие Нэша, как показал Даскалайкис, практически невозможно вычислить. Но это не означает, что поведение игроков случайно.

Рассмотрим сетку городских улиц, где водители принимают бесчисленное количество решений на десятках пересечений дорог. Даже если водители не оценивают последствия каждого возможного альтернативного решения, они, тем не менее, руководствуются несколькими простыми стратегиями. Согласно Мюнцеру Дахле, главе EECS, анализ таких систем связывает теорию игр с теорией управления, которая исследует стратегии управления динамическими системами, такими как конечности роботов и крылья самолетов.

Мюнцер Дахлеглава EECS

У нас есть другой взгляд на эти проблемы. В отличие от введения понятия равновесия и поиска соответствующих стратегий, мы наблюдаем за динамическим поведением системы и пытаемся понять, какое равновесие из него вытекает

Дахле применял методы теории игр в анализе транспортных потоков, исследуя типы дорожных систем, наиболее удобных для конкретных маршрутов. Его подход относится и к другим крупномасштабным динамическим системам, таким как электросеть.

Каждый день производители электроэнергии (атомные, угольные, ветровые и другие электростанции) предлагают новые варианты того, сколько электроэнергии они готовы производить, по какой цене и в какое время суток. Коммунальщики, которые поставляют электричество, также имеют руководителей, которые решают на основе ожидаемого потребительского спроса, сколько энергии купить у каждого поставщика. Производство энергии и ее потребление должны точно совпадать, иначе последствия будут катастрофическими.

С помощью теории игр Дахле проанализировал спрос и предложение, в результате чего выяснил, что «умные счетчики» в доме, которые могут предоставить информацию о ценообразовании на рынке электроэнергии и позволяют потребителям отложить энергоемкие домашние дела до лучших времен, действительно могут спровоцировать скачок спроса, который обрушит всю систему.

Дахле также сотрудничал с Оздаглар и ее мужем, экономистом Массачусетского технологического института Дароном Аджемоглу, чтобы проанализировать, как информация распространяется среди людей.

«Игра», в данном случае, - это ситуация, в котором люди взвешивают истинность и ложность получаемой информации в стремлении к максимальной точности собственных убеждений. "Эти вопросы изучала и социология и экономика", - говорит Оздаглар. Традиционно эти исследования предполагали, что человек может получить информацию непосредственно от любого другого человека. Однако у инженеров есть хорошо отточенные методы для анализа базовой структуры сети населения. Большинство людей, например, получают большую часть информации от своих ближайших соседей, от которых зависит ее точность.

Мюнцер Дахлеглава EECS

В прошлом, мне кажется, социальные науки и экономика подходили к проблеме иначе, чем инженеры. Сейчас мы говорим о социальных сетях, ее динамике и восприятии, вот тут, я думаю, две области и сходятся.